Programming MENACE
Recreating the Matchbox Educable Noughts and Crosses Engine for the web
🤖 Live project
📖 Portfolio project page
🗂️ Github repository
➡️ Part 2 - Training Menace
In 1961, British AI researcher Donald Michie created MENACE, the Matchbox Educable Noughts and Crosses Engine. MENACE was a mechanical computer—a computer built without electronic components—that would play noughts and crosses against a human player, improving its "choices" based on outcomes through an early, physical form of reinforcement learning.
MENACE was composed of stacks of matchboxes with unique code numbers. These code numbers mapped each box to a unique noughts and crosses game state. The empty spaces of each game state were coloured differently, and the corresponding matchbox was filled with multiple beads of each colour.
To play against MENACE, you would take the matchbox mapped to the empty game state, shake it, and pull out the tray. The colour of the bead that had landed in a small cardboard "V" within the tray was MENACE's "chosen" move, and this bead was removed. You would then find the game state depicting MENACE's move and the move you wanted to play, find the corresponding matchbox using the code number, and repeat.
If MENACE lost, the coloured beads that had been removed were not put back into the matchboxes, reducing the chance it would make those losing moves again. If MENACE won, the beads were put back in, a long with three extra beads of that colour, increasing the chance it would make those winning moves again. After a draw, the coloured beads were put back in, causing no change.
After around 150 games, MENACE was drawing consistently against human players. While MENACE never reached a 100% victory rate due to its probabilistic nature, it could reliably draw or win almost every game as it gained "experience".
The number of boxes was greatly reduced to 304 by:
- Using a single canonical state to represent all states that were reflections or rotations of eachother
- Allowing MENACE to go first
- Only including states where MENACE is next
- Excluding states with one move left, as no choice is necessary
I wanted to program a software version of MENACE as a challenge as soon as I read about it.
Others have done this, including mscroggs, whose 2016 physical copy of MENACE appeared on QI, but I wanted to solve this myself before looking at other solutions.
Stack
The frontend of our MENACE application won't use a framework, just HTML, CSS, and Vanilla JavaScript. We'll use the socket.io client library for low-latency communication with our server.
Our server will be a Node.js express server. Socket.io will allow us to create different games for different connections.
Server-side
Canonical Boards
Boards will be represented in our code by an array of 0s, 1s, and 2s, where 0 represents an empty space, 1 represents a O, and 2 represents an X.
let exampleBoard = [2, 0, 0, 1, 0, 0, 0, 2, 0];
// -represents- -indices-
// _x_|___|___ _0_|_1_|_2_
// _o_|___|___ _3_|_4_|_5_
// | x | 6 | 7 | 8 Just like Donald's matchbox computer, our application will use a single canonical board to represent all boards that can be reflected or rotated into that canonical board.
In geometry, the group of symmetries of a square is represented by D4, which consists of four rotations (by 0°, 90°, 180°, and 270°) and four reflections (across axes of symmetry). Performing a rotation followed by a reflection is known as an 'Improper Rotation.' These result in duplicate symmetries, as colour-coded in the image below. Therefore, we only need to consider the eight distinct transformations (the ones in the top row and left column below), not every combination of them.
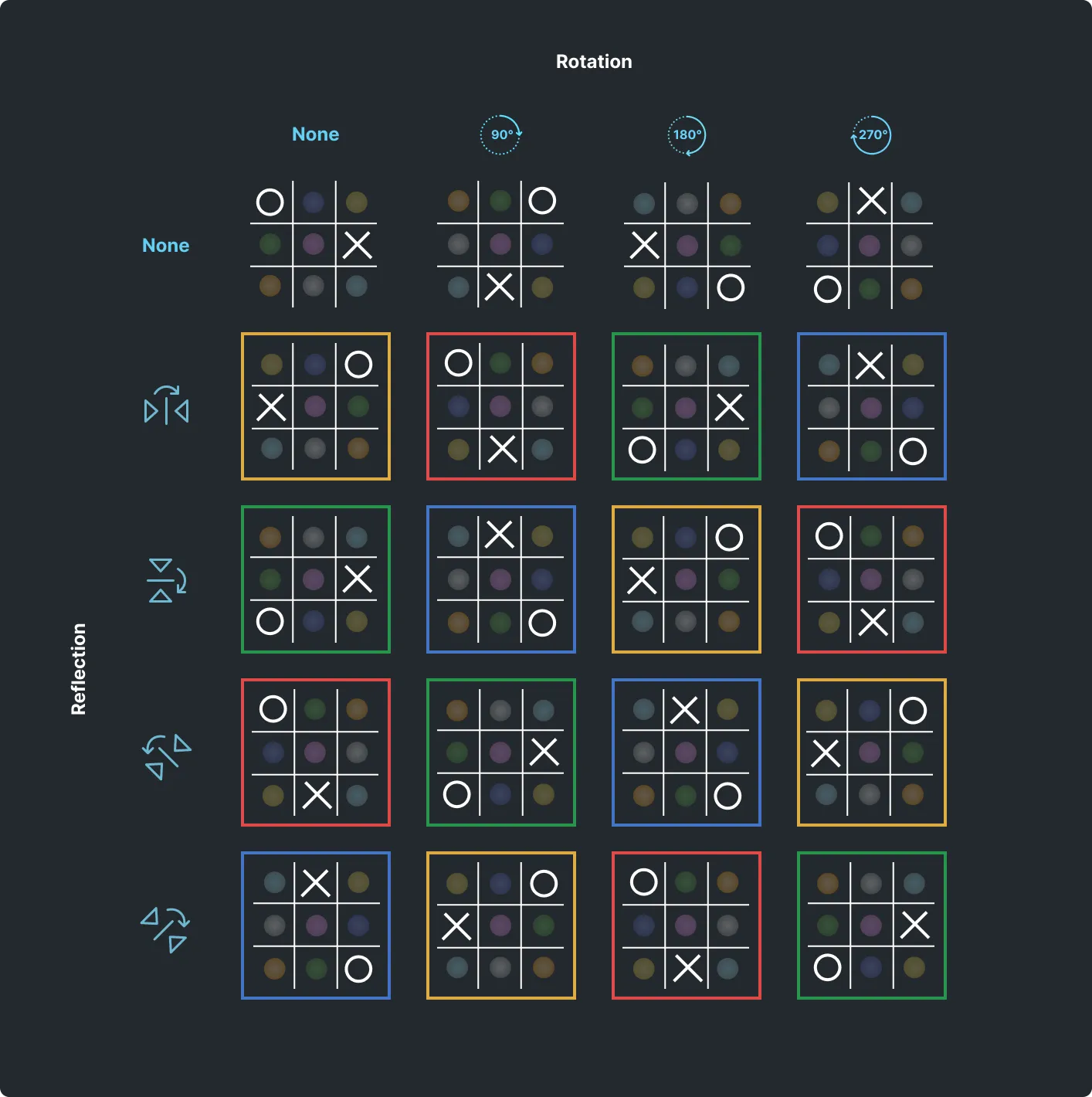
The canonical board will be the board whose array has the first unique smallest element.
💡 Because we're using integers, modern JavaScript engines like V8 (used in Chrome and Node.js) will classify our array elements as "Packed Smi Elements", where "Smi" stands for "small integers"/"small immediates". This allows an optimisation where our raw integer values are actually stored contiguously in memory. If we were to use strings such as "x", "o", and "-", our elements would be spread out in memory, and the array would contain pointers to those elements. We'll be reflecting and rotating game state arrays to and from their canonical forms a lot, both during the recursive building of our decision graph and in every turn of each game, so the small integer optimisation is good, especially considering socket.io will create multiple games - one for each connected user. 💡
Working with canonical boards introduces a few challenges, so let's prove it's worth it. I wrote a function that returns all valid game states, and how many of those are relevant to MENACE.
function generateAllBoards(
board = [0, 0, 0, 0, 0, 0, 0, 0, 0],
xTurn = false,
depth = 0
) {
let boards = 0;
let menaceTurns = 0;
// Skip boards with only one turn left
if (depth >= 7) return { boards, menaceTurns };
for (let i = 0; i < 9; i++) {
if (board[i] === 0) {
let newBoard = [...board];
newBoard[i] = xTurn ? 2 : 1;
if (checkOutcome(newBoard) === null) {
boards++;
if (xTurn) menaceTurns++;
const childResults = generateAllBoards(newBoard, !xTurn, depth + 1);
boards += childResults.boards;
menaceTurns += childResults.menaceTurns;
}
}
}
return { boards, menaceTurns };
}
const { boards, menaceTurns } = generateAllBoards();
console.log(`There are ${boards} boards in our graph.`);
console.log(`${menaceTurns} of those are relevant to MENACE.`);There are 166905 boards in our graph.
52488 of those are relevant to MENACE.I did exclude boards where there's only one turn left, as these boards would not require training.
So, there would be 52,488 nodes relevant to MENACE, containing probabilities MENACE will choose each of their child nodes. Without canonical forms, each of these 52,488 nodes would have to be visited several times for their respective probabilities to be updated sufficiently, so you can imagine how many games would have to be played for this model to "learn". The probabilities of the following moves would have to be updated separately, despite them being logically identical:
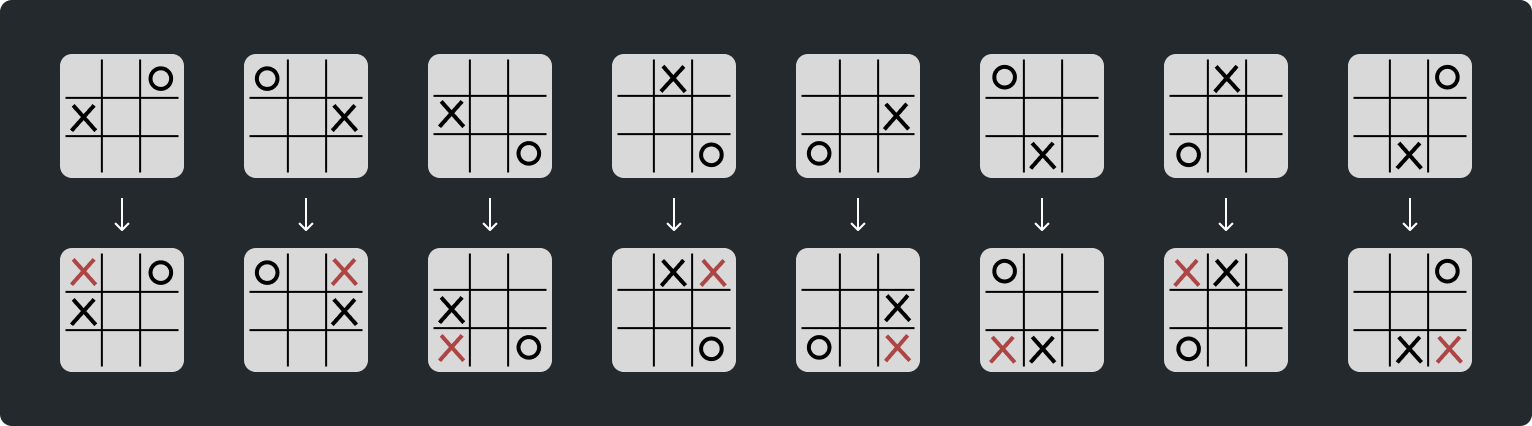
We also need to consider that, even when building a graph of only canonical boards, several boards can have identical children. As an example, here are eight states that share a child with the corresponding boards in the previous image:
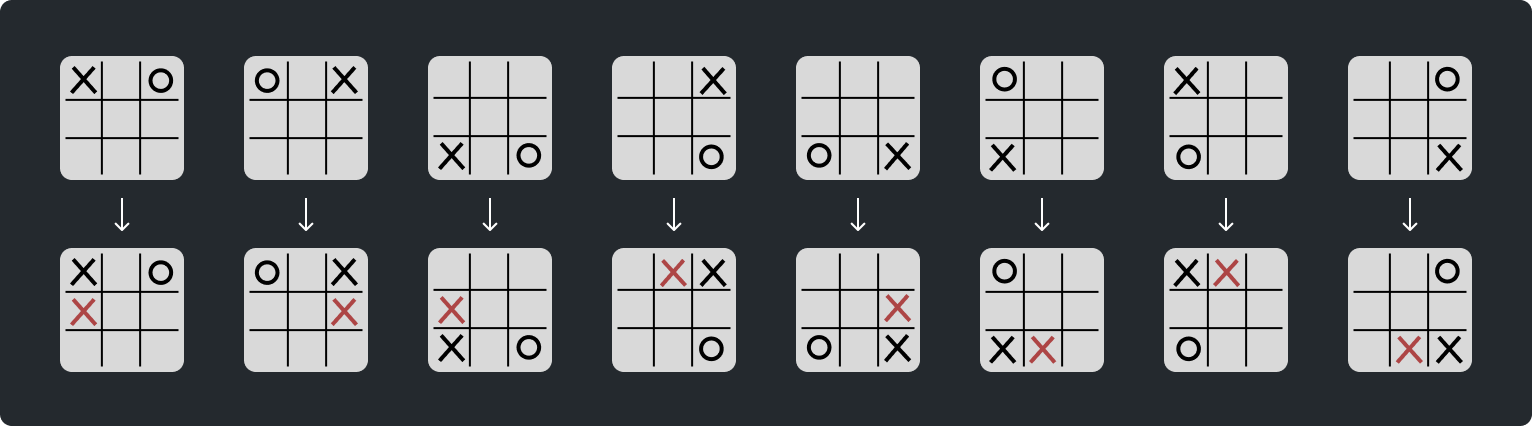
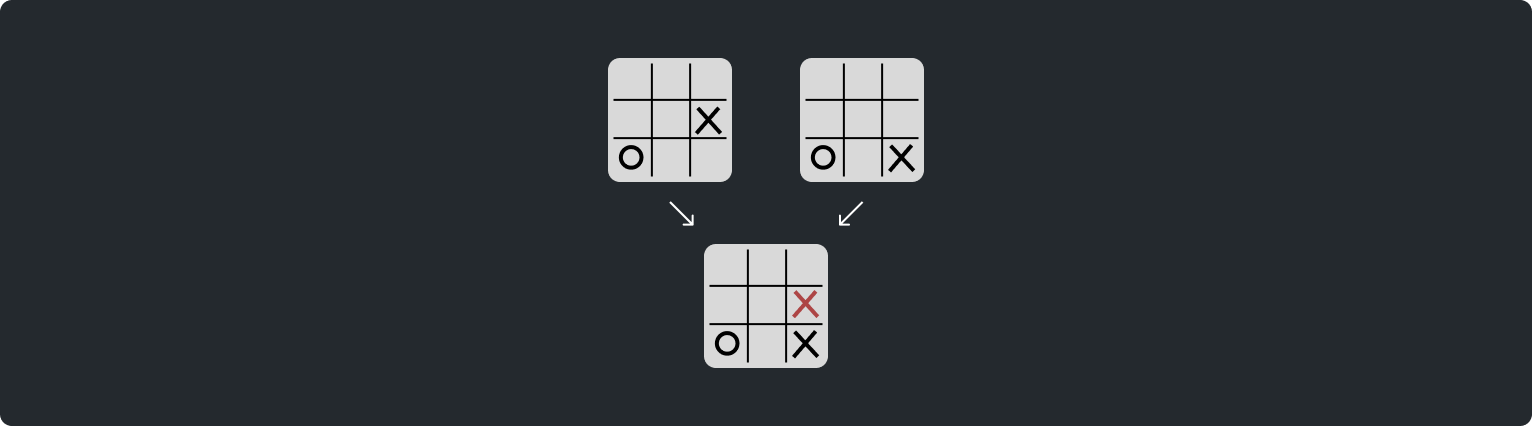
Duplicate canonical children could share the same probabilities, but each parent having its own copy of a canonical child is a waste of space, so we'll have parent nodes with shared children reference the same child in memory.
In our graph, all 16 moves in the two previous images will be represented as:
Let's look at how we'll transform state arrays into their canonical form in code.
Transformations
In a transformation folder, I'm going to create a folder called transformations, which contains the files transformationMappings.js and transformationFunctions.js.
transformationMappings.js contains a 2D array. In the inner arrays, each index represents a specific tile, and the value at that index indicates the new index of the tile after applying a reflection or rotation.
const transformationMapping = [
[0, 1, 2, 3, 4, 5, 6, 7, 8], // identity (no rotation)
[2, 5, 8, 1, 4, 7, 0, 3, 6], // rotate 90
[8, 7, 6, 5, 4, 3, 2, 1, 0], // rotate 180
[6, 3, 0, 7, 4, 1, 8, 5, 2], // rotate 270
[6, 7, 8, 3, 4, 5, 0, 1, 2], // vertical reflection
[2, 1, 0, 5, 4, 3, 8, 7, 6], // horizontal reflection
[8, 5, 2, 7, 4, 1, 6, 3, 0], // top left to bottom right reflection
[0, 3, 6, 1, 4, 7, 2, 5, 8], // top right to bottom left reflection
];The vertical reflection array moves the tile at index 0 to index 6, the tile at index 1 to index 7, etc.
transformationFunctions.js will contain our getCanonicalForm function and all of the transformation helpers it uses:
function applyTransformation(board, transformationIndex) {
const mapping = transformationMapping[transformationIndex];
return board.map((_, idx) => board[mapping[idx]]);
}
function isLessThan(arr1, arr2) {
for (let i = 0; i < arr1.length; i++) {
if (arr1[i] < arr2[i]) {
return true;
} else if (arr1[i] > arr2[i]) {
return false;
}
}
return false;
}
function getCanonicalForm(board) {
let canonicalBoard = board.slice();
let transformationKey = 0; // default to identity transformation index
for (let i = 0; i < transformationMapping.length; i++) {
const transformedBoard = applyTransformation(board, i);
if (isLessThan(transformedBoard, canonicalBoard)) {
canonicalBoard = transformedBoard.slice();
transformationKey = i;
}
}
return {
canonicalBoard,
transformationKey,
};
}It'll now be much easier to manipulate states.
Notice how in our getCanonicalForm function, we're returning the key (index) of the transformation array used to get the input board to its canonical form. We'll see why when we build and traverse our decision graph.
Classes
There'll be two classes in our server-side game logic:
- The
BoardStateclass, which will build our graph of board states recursively - The
MENACEclass, which will be instantiated for each game and play by traversing the graph of board states
The BoardState Class
The BoardState class will build our graph recursively using a generateChildren method.
Because state nodes in our data structure will share child states and have multiple parents, our decision data structure will be a "directed acyclic graph", or DAG. The graph will be traversed in one direction (hence "directed") and no sequence of edges will form a closed loop (hence "acyclic").
Let's implement a BoardState class whose generateChildren function:
- Uses
getCanonicalFormto make sure every child state generated is canonical - Uses a JavaScript map to keep track of the states that already exist, so that other nodes can reference the same object in memory as a child
class BoardState {
constructor(
state = Array(9).fill(0),
xTurn = true,
loadData = {},
statesSeenMap,
depth = 0
) {
this.state = state;
this.key = state.join("");
this.xTurn = xTurn;
this.childStateChances = {};
this.childLinks = [];
this.loadData = loadData;
this.outcome = checkOutcome(this.state);
this.statesSeenMap = statesSeenMap || new Map();
this.depth = depth;
this.generateChildren();
}
generateChildren() {
if (this.outcome != null) {
return;
}
this.state.forEach((place, index) => {
if (place == 0) {
let childState = [...this.state];
childState[index] = this.xTurn ? 2 : 1;
let { canonicalBoard, transformationKey } =
getCanonicalForm(childState);
let childStateKey = canonicalBoard.join("");
if (this.childExistsOnThisNode(childStateKey)) {
return;
}
if (this.statesSeenMap.has(childStateKey)) {
let childFromMap = this.statesSeenMap.get(childStateKey);
this.addChild(childFromMap, transformationKey);
} else {
let newChildState = new BoardState(
canonicalBoard,
!this.xTurn,
this.loadData,
this.statesSeenMap,
this.depth + 1
);
this.statesSeenMap.set(childStateKey, newChildState);
this.addChild(newChildState, transformationKey);
}
this.loadChildProbabilities(childStateKey);
}
});
}
// ... cont'd
}Before looking at some of the logic that has been abstracted away for readability, lets see how many nodes are in this graph, and how many are relevant to MENACE.
To calculate the total nodes, we can just log the size of statesSeenMap.
let testRoot = new BoardState();
console.log(testRoot.statesSeenMap.size);764There are 764 total nodes representing canonical states in our graph. There are more nodes than there were matchboxes in the original MENACE because we're building out nodes for both player's turns. This will allow us to train both sides of the game and switch up who goes first in future.
For now, we'll let MENACE go first as in the original.
To calculate the nodes relevant to MENACE, we can increment a temporary global counter in the constructor of BoardState whenever it's X's turn, there's no outcome, and there's more than one move left.
// global
let menaceTurns = 0;
// in BoardState constructor:
if (this.xTurn && !this.outcome && this.depth < 7) {
menaceTurns++;
}
// global
let testRoot = new BoardState();
console.log(menaceTurns);304Reassuringly, this reveals there are 304 states relevant to MENACE when it goes first, just like in the original MENACE.
Let's look more closely at the generateChildren method.
The constructor gives each node a key string, which is the result of calling .join("") on a board state array. It's used for comparison, and as a key in statesSeenMap, childStateChances, and loadData, all explored later. Saving this key in the constructor prevents us having to call .join("") during games.
childExistsOnThisNode is simple enough:
childExistsOnThisNode(childStateKey) {
return this.childLinks.some(childLink => childLink.child.key === childStateKey);
}Whether an existing state is retrieved from the map or a new state is created, it's passed to the same addChild method:
addChild(childState, transformationKey) {
this.childLinks.push({
transformationByParent: transformationKey,
child: childState,
});
}As you can see, each node's this.childLinks is an array of objects that contain not only a reference to the child state node, but the key of the transformation used by the parent to get that canonical child. This will be essential for trasforming between the canonical board states MENACE works with and the visual board state the player expects to see.
We can conceptualise these childLink objects as the "edges" of our graph:
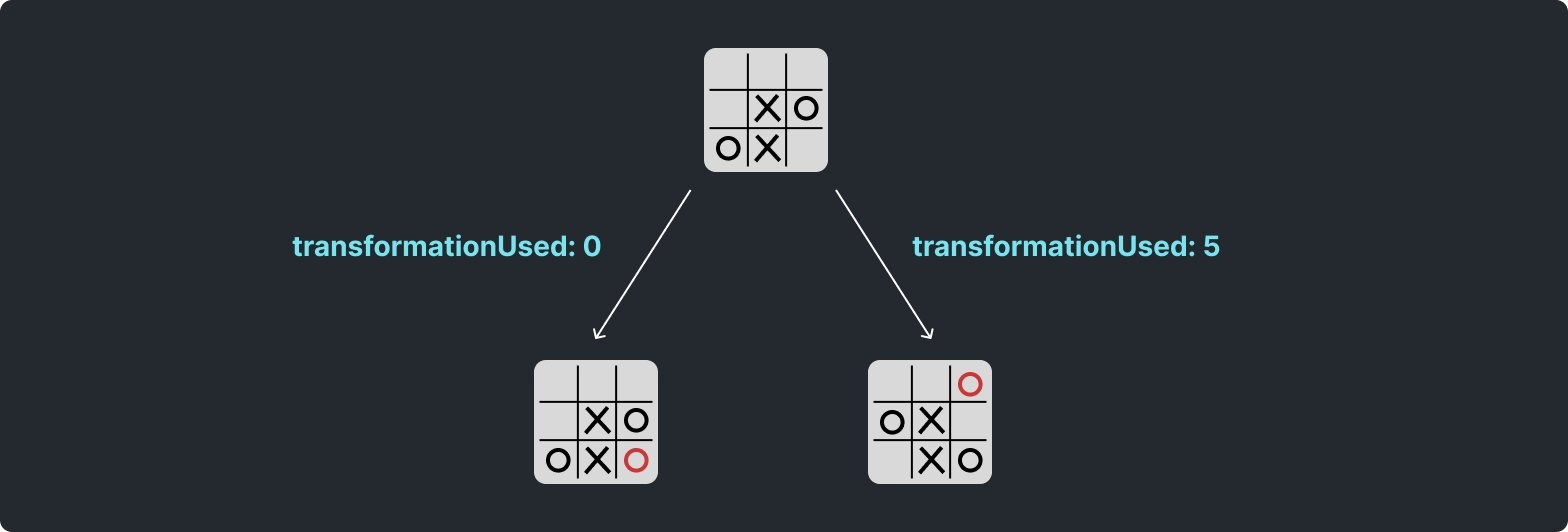
Finally, loadChildProbabilities will either load the probability a child will be chosen, or initialise it to 3:
loadChildProbabilities(childStateKey) {
if (this.loadData && childStateKey in this.loadData) {
this.childStateChances[childStateKey] = this.loadData[childStateKey];
} else {
this.childStateChances[childStateKey] = 3;
}
}We'll look at how loadData is saved and retrieved in my next post, Training Menace, but for now know that the childStateChances object looks like this:
{
'000000002': 3,
'000000020': 3,
'000020000': 3
}The MENACE Class
The second class will be MENACE itself. An instance will be created for each game, and when moves are made, MENACE will update a currentState reference, traversing the canonical states in the BoardState graph. MENACE will also keep track of the visualState - the potentially non-canonical state from the player's perspective.
We've laid the foundations to be able to map between the visual state and the canonical state easily as the game is played. Every node in our graph contains the transformation used to reach each child's canonical form. This means that after MENACE has converted the player's chosen move to canonical form and chosen its own move, it can undo transformations to send the result back in the form the player expects.
The high-level flow of transformations in the MENACE class's makeMove function will be:
These two transformations save us hundreds of thousands of nodes.
Our menace class will have methods for:
- Receiving a player move and making a move, checking for an outcome after each (as in the image above)
- Training (updating probabilities) if there is an outcome
- Resetting for a new game
MENACE's constructor and reset method are really simple:
class Menace {
constructor(root, iAmX = true) {
this.visualState = Array(9).fill(0);
this.root = root;
this.iAmX = iAmX;
this.currentState = root;
this.statesThisGame = [root];
if (this.iAmX) {
this.makeFirstMove();
}
}
reset() {
this.visualState = Array(9).fill(0);
this.currentState = this.root;
this.statesThisGame = [this.root];
if (this.iAmX) {
this.makeFirstMove();
}
}
// ... cont'd
}iAmX will let us parameterise who goes first.
I'll go through our makeMove method in two parts. First, let's go over the first part of the method, which deals with the player's chosen move:
MakeMove(playerMoveIndex) {
if (this.visualState[playerMoveIndex] != 0) {
return this.moveError("The chosen tile was not empty");
}
let visualStateCopy = [...this.visualState];
visualStateCopy[playerMoveIndex] = this.iAmX ? 1 : 2;
let { canonicalBoard, transformationKey } =
getCanonicalForm(visualStateCopy);
let playerStateKey = canonicalBoard.join("");
let foundChild = this.moveToChildByKey(playerStateKey);
if (!foundChild) {
return this.moveError("No matching child state found");
}
if (this.currentState.outcome != null) return this.endGame();
// ... cont'd belowIf the player's move is valid we update a copy of the visual state. We then transform this to it's canonical form and update the current state with moveToChildByKey:
moveToChildByKey(childKey) {
const matchingChildLink = this.currentState.childLinks.find(
(childLink) => childLink.child.key === childKey
);
if (matchingChildLink) {
this.currentState = matchingChildLink.child;
this.statesThisGame.push(this.currentState);
}
return matchingChildLink;
}This ensures the state is not tampered with on the client. If the player chooses a tile that is not empty or if moveToChildByKey returns undefined, we return the result of the moveError method.
moveError(message) {
return {
state: null,
outocme: null,
error: message,
};
}Our frontend will display errors whenever a null state is returned.
Next, we push the player's move to this.statesThisGame (so that we can train the player's moves, too), and check for an outcome. If there is an outcome, we return this.endGame():
endGame() {
let savedState = [...this.visualState];
let savedOutcome = this.currentState.outcome;
this.train();
this.reset();
return {
state: savedState,
outcome: savedOutcome,
};
}The second part of the makeMove function deals with MENACE's turn.
let menaceChoiceKey = weightedRandomChoice(
this.currentState.childStateChances
);
let menaceChoiceLink = this.moveToChildByKey(menaceChoiceKey);
// undo transformations parent used to generate current state
let stateInParentForm = reverseTransformation(
this.currentState.state,
menaceChoiceLink.transformationByParent
);
// undo transformations to get from visual state to parent state
let stateInVisualForm = reverseTransformation(
stateInParentForm,
transformationKey
);
this.visualState = stateInVisualForm;
if (this.currentState.outcome != null) return this.endGame();
return {
state: this.visualState,
outcome: null,
};
}MENACE makes a weighted random choice based on the current node's childStateChances and updates currentState to the relevant child. It then reverses all transformations to get the new visual state, again checking for an outcome.
We'll look at the train method in my next post, Training Menace.
Exress Server
Leaving out the server boilerplate code, which can be found in the Github repository, here's our socket in server.js:
// data
let data = loadData();
// decision graph
let root = new BoardState(undefined, undefined, data);
root.generateChildren();
const games = {};
io.on("connection", (socket) => {
console.log(`User connected: ${socket.id}`);
socket.on("startGame", () => {
console.log(`Starting game for user ${socket.id}`);
let menaceFirst = true;
let menace = new Menace(root, menaceFirst);
games[socket.id] = menace;
socket.emit("gameStarted", menace.visualState);
});
socket.on("makeMove", (move) => {
const menace = games[socket.id];
if (!menace) {
socket.emit("error", "Game not found. Please start a new game.");
return;
}
let chosen_id = move.space_id;
let response_state = menace.MakeMove(chosen_id);
socket.emit("moveMade", {
outcome: response_state.outcome,
state: response_state.state,
});
});
socket.on("reset", () => {
let menace = games[socket.id];
socket.emit("gameStarted", menace.visualState);
});
socket.on("disconnect", () => {
console.log(`User disconnected: ${socket.id}`);
delete games[socket.id];
});
});
app.get("/", (req, res) => {
res.sendFile(path.join(__dirname, "public", "index.html"));
});For now, menaceFirst is hardcoded in the socket connection callback.
The loadData function reads and parses saved probabilities from a loadData.json file if one exists. If not it returns an empty object.
function loadData() {
try {
const data = fs.readFileSync("loadData.json", "utf-8");
if (data) {
return JSON.parse(data);
} else {
console.log("No data from load file");
return {};
}
} catch (err) {
console.error(
"A load file was not read - the load file should be called loadData.json (utf-8)"
);
return {};
}
}Frontend
Serving the HTML from the same server as our game logic allows us to use the socket.io client library easily:
<script src="/socket.io/socket.io.js"></script>In our client JavaScript, we can first initialise state variables and grab the DOM elements we need. Then we can add listeners to our spaces to emit "makeMove" on click, sending the space index to the server as the space_id:
const socket = io("http://localhost:3000");
let visual_state = [];
let loading = false;
let resultDisplay = document.getElementById("result-display");
let errorDisplay = document.getElementById("error-display");
let resultTimeout;
let errorTimeout;
let resetError = () => {
errorDisplay.style.display = "none";
errorDisplay.innerHTML = "";
};
let resetResult = () => {
resultDisplay.style.display = "none";
resultDisplay.innerHTML = "";
};
let spaces = document.querySelectorAll(".space");
spaces.forEach((space) => {
space.addEventListener("click", async (e) => {
if (!loading) {
loading = true;
let id = e.target.getAttribute("id");
socket.emit("makeMove", { space_id: id });
}
});
});We can then emit startGame on page load and add our socket listeners.
socket.emit("startGame");
socket.on("gameStarted", (state_array) => {
visual_state = state_array;
updateBoard(state_array);
});
socket.on("moveMade", (new_state_object) => {
if (errorTimeout) clearTimeout(errorTimeout);
resetError();
resetResult();
if (new_state_object.state == null) {
errorDisplay.innerHTML = new_state_object.error;
errorDisplay.style.display = "grid";
// debounce error
errorTimeout = setTimeout(resetError, 3000);
loading = false;
}
if (new_state_object.outcome != null) {
if (resultTimeout) clearTimeout(resultTimeout);
resultDisplay.style.display = "grid";
resultDisplay.innerHTML = `${new_state_object.outcome}`;
resetBoard();
socket.emit("reset");
resultTimeout = setTimeout(resetResult, 3000);
loading = false;
} else {
updateBoard(new_state_object.state);
loading = false;
}
});
socket.on("disconnect", () => {
console.log("Disconnected from server");
});This is everything we need to start playing against MENACE!
I've decided to make a separate post about Training Menace, where we'll look into training strategies more broadly and explore some machine learning terminology along the way.
Thank you for reading, and I hope you learned something or just enjoyed reading through my thinking on this. 😁🎲